Iroh blobs is a very efficient way to distribute data from one peer to another. It even has some capabilities to get data from multiple nodes, as of iroh-blobs 0.9x. But there is one crucial component missing for it to become a global permissionless content distribution system: a content discovery service that tells you which nodes have which content.

This is a very hard problem. Existing systems such as bittorrent solve it reasonably well, although they are not perfect.

The standard solution for content discovery in systems such as bittorrent and IPFS is a distributed hash table. This series of blog posts and the associated repository are an experiment: is it possible to write a high performance distributed hash table using iroh connections?

The code is not yet production ready, but it is an interesting use case for many advanced techniques involving iroh connections, such as connection pools and 0rtt connections. It also is a nice way to show off irpc, both for local rpc to control a DHT node and for the DHT protocol itself.

What is a distributed hashtable

Let's see what wikipedia says:

"A distributed hash table (DHT) is a distributed system that provides a lookup service similar to a hash table. Key–value pairs are stored in a DHT, and any participating node can efficiently retrieve the value associated with a given key. The main advantage of a DHT is that nodes can be added or removed with minimum work around re-distributing keys."

So a distributed hash table seen as a black box is just like a hashtable, but spread over possibly millions of machines that are connected via possibly slow and fallible network connections. The algorithm needs to gracefully deal with nodes being slow or low latency, nodes coming and going, and ideally even with some nodes that intentionally misbehave.

Keys

Just like a normal hashtable, a distributed hashtable maps some key type to some value type. Keys in local hashtables can be of arbitrary size. The key that is actually used for lookup is a (e.g. 64 bit) hash of the value, and the hashtable has additional logic to deal with rare but inevitable hash collisions. For distributed hash tables, typically you restrict the key to a fixed size and let the application deal with the mapping from the actual key to the hashtable keyspace. E.g. the bittorrent mainline DHT uses a 20 byte keyspace, which is the size of a SHA1 hash. The main purpose of the mainline DHT is to find content providers for data based on a SHA1 hash of the data. But even with mainline there are cases where the actual key you want to look up is larger than the keyspace, e.g. bep_0044 where you want to look up some information for an ED25519 public key. In that case mainline does exactly what you would do in a local hashtable - it hashes the public key using SHA1 and then uses the hash as the lookup key.

For iroh we are mainly interested in looking up content based on its BLAKE3 hash. Another use case for the DHT is to look up information for an iroh node id, which is an ED25519 public key. So it makes sense for a clean room implementation to choose a 32 byte keyspace. An arbitrary size key can be mapped to this keyspace using a cryptographic hash function with an astronomically low probability of collisions.

Values

In principle, values in a DHT can be of arbirary size. But there are various reasons for wanting to keep the values small.

First of all, we want requests to store and look up data to be small for efficiency. Ideally a storage or lookup request should fit into a single network packet even with the inevitable framing overhead. In QUIC, the minimum MTU (maximum transmission unit) is specified as 1200 bytes. So if a request consisting of key, value and some overhead fits into 1200 bytes, a request or response will be sent as a single non-fragmented UDP packet.

Second, we rely on arbitrary nodes on the network to store data for us without being in any way compensated for it. So the values need to be small so a small DHT node can store many of them. If the value size was unlimited, people could and would abuse the DHT for storing actual data, which would put a lot of load on DHT nodes and would make it extremely unlikely that people would run DHT nodes without being compensated for it.

For that reason, mature systems such as the mainline DHT restrict value size to 1000 bytes, and we are going to limit value size to 1024 bytes or 1KiB.

You could write a DHT to store arbitrary values, but in almost all cases the value should have some relationship with the key. E.g. for mainline, the value in most cases is a set of socket addresses where you can download the data for the SHA1 hash of the key. So in principle you could validate the key by checking if you can actually download the data from the socket addresses contained in the data. In some mainline extensions, like bep_0044, the key is the SHA1 hash of an ED25519 public key, and the value contains the actual public key, a signature computed from the corresponding private key, and some user data. Again, it is possible to validate the value based on the key - if the SHA1 hash of the public key contained in the value does not match the lookup key, the value is invalid for the key.

Storage

Even disregarding all the distributed systems complexity, at the end of the day the data needs to live somewhere. Each node will store a fraction of the total data. So one component of a DHT node is just a remotely accessible key value store, where the key is a fixed size blob. There can be multiple values for a key. E.g. there can be multiple nodes that store the same data. For that reason the storage is a multimap. The storage layer needs to have some mechanism to limit the number of values for a key, typically by time based expiry and/or a maximum number of values per key.

Routing

As mentioned above, in a DHT not every node has all the data. So we need some mechanism to find which node has the data. Basically we need a way for a node to say "I don't have the data, but you might try my neighbours X and Y, they are more likely to have it". Independent of the exact routing algorithm, it is important to understand that routing is only concerned with keys, not with values. You first find the nodes that are most likely to have a value for a key, then ask these nodes for the actual value. So the two parts, routing and value storage/retrieval should be pretty separate. Adding new value types should be possible without having to touch the routing algorithm, and modifying the routing algorithm should be possible without having to think about values at all.

Kademlia

The most popular routing algorithm for DHTs is Kademlia. The core idea of kademlia is to define a metric that gives a scalar distance between any two keys (points in the metric space) that fulfills the metric axioms. DHT nodes have a node id that gets mapped to the metric space, and you store the data on the k nodes that are closest to the key.

The metric chosen by kademlia is the XOR metric: the distance of two keys a and b is simply the bitwise xor of the keys. This is absurdly cheap to compute and fulfills all the metric axioms. It also helps with sparse routing tables, as we will learn later.

If a node had perfect knowledge of all other nodes in the network, it could give you a perfect answer to the question "where should I store the data for key key". Just sort the set of all keys that correspond to node ids by distance to the key and return the k smallest values. For small to medium DHTs this is a viable strategy, since modern computers can easily store millions of 32 byte keys without breaking a sweat. But for either extremely large DHTs or nodes with low memory requirements, it is desirable to store just a subset of all keys.

A fixed size random sampling of the set of all known node ids would be viable and would work, but there are some downsides. For a completely random sampling, you do not have detailed knowledge of your immediate neighbours, so it would take many hops to find a better node if you are already close to the goal. If the sampling was only neighbours in terms of the distance metric, it would take you many hops to find a node that is far away. It turns out that the best distribution is a power law distribution where you know a lot of immediate neighbours but also some nodes that are far away.

Imagine you wanted to find an arbitrary person, and your entire friend group was geographically close. It would be a lot of hops to find somebody that is far away. Now imagine your entire friend group was randomly spread around the world. It would take a lot of hops to find a neighbour that is not in your friend group. The ideal friend distribution is to know a lot of people in your village, but also some people in the next city, in neighbouring countries, and a few on different continents.

Kademlia uses a routing table that remembers nodes based on proximity. It defines proximity buckets based on the number of leading zeros of the xor distance to your own node id. For a k-bit keyspace there are k proximity buckets, and for each of these so called k-buckets you have a maximum number of nodes you will remember. This gives a fixed upper limit on the size of the routing table while automatically keeping a power law distribution. You will know almost all nodes in your immediate proximity, but also some nodes that are on the other side of the world in terms of the xor metric space. The way the bucketing is done is quite cheap, but other schemes would work just as well as long as you approximate a power law distribution. E.g. you could also have 32 buckets based on the number of trailing zero bytes in the distance, and increase the bucket size.

Lookup algorithm

If each node had perfect knowledge of all other nodes on the network, lookup and storage would be just a two step process:

1. Ask any node for the k closest nodes to key x.
2. Store/look up the data on these k nodes.

But since this is no longer the case, the lookup process needs to be iterative. We first use our local knowledge to find good candidates to ask, then ask them for the k closest nodes to our target x that they knows. We then ask some of the resulting nodes the same question again, until we can no longer make an improvement. Basically we do a greedy downhill search until we arrive at a minimum, which due to the power law distribution of the nodes is hopefully a global minimum. There are some intricacies to this iterative algorithm. E.g. we always ask multiple nodes at each stage, while keeping the parallelism limited to avoid having too many concurrent connections. Fortunately these complexities don't leak into the protocol. All we need is a way to ask a node for the k closest nodes to some key x according to its local knowledge.

Routing table updates

A key property of a DHT compared to more rigid algorithms is that nodes should be able to come and go at any time. So you update the routing tables whenever you interact with a different node id of a DHT node. In addition you actively query the network with random keys to learn about new node ids. We will perform some experiments with various updating schemes later.

RPC protocol

Now that we have a very rough idea what a distributed hashtable is meant to do, let's start defining the protocol that nodes will use to talk to each other. We are going to use irpc to define the protocol. This has the advantage that we can simulate a DHT consisting of thousands of node in memory initially for tests, and then use the same code with iroh connections as the underlying transport in production.

First of all, we need a way to store and retrieve values. This is basically just a key value store API for a multimap. This protocol in isolation is sufficient to implement a tracker, a node that has full knowledge of what is where.

Values

An id is just a 32 byte blob, with conversions from iroh::NodeId and blake3::Hash.

pub struct Id([u8; 32]);

A value can be a bunch of different things, all related to the key. Either a provider for a BLAKE3 hash, a message signed by an Ed25519 key, or a tiny blob of BLAKE3 hashed data. Each of these variants corresponds to a mainline feature.

pub enum Value {
    Blake3Provider(Blake3Provider),
    ED25519SignedMessage(ED25519SignedMessage),
    Blake3Immutable(Blake3Immutable),
}

We want the ability to query only values of a certain kind, so we need a corresponding Kind enum:

pub enum Kind {
    Blake3Provider,
    ED25519SignedMessage,
    Blake3Immutable,
}

KV store protocol

For the kv store part of the DHT rpc protocol, we want to keep things extremely minimalistic. So we just need a way to set and get values.

pub struct Set {
    pub key: Id,
    pub value: Value,
}

pub struct GetAll {
    pub key: Id,
    pub kind: Kind,
    ...
}

Set allows us to ask the node to store a value. It might refuse to do so, but we can ask. GetAll allows us to get all values of a certain kind. That's it. So here is the storage and retrieval part of our protocol:

    #[rpc_requests(message = RpcMessage)]
    pub enum RpcProto {
        /// Set a key to a value.
        #[rpc(tx = oneshot::Sender<SetResponse>)]
        Set(Set),
        /// Get all values of a certain kind for a key, as a stream of values.
        #[rpc(tx = mpsc::Sender<Value>)]
        GetAll(GetAll),
        ... // routing part TBD
    }

So let's take a look at the rpc annotations. Set is a normal RPC call with a single answer message of type SetResponse, which just contains some info about if the set was successful and if not why not. GetAll might return many values, so we use a response stream of Values. The #[rpc_requests(message = RpcMessage)] annotation is to turn this enum into an irpc rpc protocol and to define a corresponding message enum. For details, see this blog post about irpc.

GetResponse is still missing. It's just an enum describing if the set succeeded, and if not why it failed. You might wonder why we don't use a Result<(), SetError>: you could do that, but you have to be aware that serializing detailed errors is sometimes a big pain, and also the exact details of the failure like the stack trace are nobody's business. We just give you a very rough idea why the request failed so you can decide whether to try again or not. E.g. ErrFull means you might try a bit later, ErrInvalid means that there is something wrong with the value, e.g. signature error, and there is no point in trying again.

pub enum SetResponse {
    Ok,
    /// The key was too far away from the node id in terms of the DHT metric.
    ErrDistance,
    /// The value is too old.
    ErrExpired,
    /// The node does not have capacity to store the value.
    ErrFull,
    /// The value is invalid, e.g. the signature does not match the public key.
    ErrInvalid,
}

Routing protocol

The routing part of the protocol is a bit more interesting. We want the ability to query a node for its local knowledge of nodes for a key. So the message needs to contain the key we are looking for. But there is one more thing: if the requester is itself a DHT node, the callee might want to add this node id to its routing table. If the requester is a short lived client, we don't want its node id to be added to the routing table since asking it anything would be pointless. It is up to the callee to validate that the id is a valid responsive DHT node and then update its routing table, all we do in the request is to provide this information.

Note that for a mem transport there is no way for the callee to check the requester node id. For the rpc protocol, the mem transport is only used in simulations where we trust the caller. When the request comes in via an iroh connection, we can do a quick check that the requester node id is the remote node id of the connection.

pub struct FindNode {
    pub id: Id,
    pub requester: Option<NodeId>,
}

Now let's add this message to the rpc protocol:

#[rpc_requests(message = RpcMessage)]
pub enum RpcProto {
    ...
    /// A request to query the routing table for the most natural locations
    #[rpc(tx = oneshot::Sender<Vec<NodeAddr>>)]
    FindNode(FindNode),
}

The answer is just a sequence of iroh NodeAddrs, containing most importantly the node id of the nodes, but also information like the current home relay and possibly even socket addrs where you can attempt to dial the node. Of course we could rely on node discovery here, but DHTs will perform a lot of connections to a very large number of nodes, and the callee already has some information about how to dial the node, so we might as well include it to reduce the load on the node discovery system.

You might ask why this is not a streaming response but just a single Vec. The number of nodes a node will return in response to a FindNode query is very small (at most ~20), and is immediately available after querying the routing table. So there is no point in streaming this - 20 NodeAddrs with some discovery info will fit into 1 or 2 MTUs, so it is more efficient to send them all at once.

And that's it. That is the entire rpc protocol. Many DHT implementations also add a Ping call, but since querying the routing table is so cheap, if you want to know if a node is alive you might as well ask it for the closest nodes to some random key and get some extra information for free.

RPC client

Using an irpc client directly is not exactly horrible, but nevertheless we want to add some sugar to make it more easy to use. So we write a wrapper around the irpc client that makes using it more convenient. Set and FindNode are just async fns, GetAll returns a stream of responses.

impl RpcClient {
    ...

    pub async fn set(&self, key: Id, value: Value) -> irpc::Result<SetResponse> {
        self.0.rpc(Set { key, value }).await
    }

    pub async fn get_all(
        &self,
        key: Id,
        kind: Kind,
    ) -> irpc::Result<irpc::channel::mpsc::Receiver<Value>> {
        self.0
            .server_streaming(GetAll { key, kind }, 32)
            .await
    }

    pub async fn find_node(
        &self,
        id: Id,
        requester: Option<NodeId>,
    ) -> irpc::Result<Vec<NodeAddr>> {
        self.0.rpc(FindNode { id, requester }).await
    }
}

This client can now be used either with a remote node that is connected via a memory transport, or with a node that is connected via an iroh connection.

Storage implementation

The first thing we would have to do to implement this protocol would be the storage part. For this experiment we will just use a very simple memory storage. This might even be a good idea for production! We have a limited value size, and DHTs are not persistent storage anyway. DHT records need to be continuously republished, so if a DHT node goes down it will just be repopulated with values shortly after becoming online again.

The only notable thing we do here is to store values for different value kinds separately for more simple retrieval, and to use an IndexSet for the values to keep values sorted by insertion time.

struct MemStorage {
    /// The DHT data storage, mapping keys to values.
    /// Separated by kind to allow for efficient retrieval.
    data: BTreeMap<Id, BTreeMap<Kind, IndexSet<Value>>>,
}

impl MemStorage {
    fn new() -> Self {
        Self {
            data: BTreeMap::new(),
        }
    }

    /// Set a value for a key.
    fn set(&mut self, key: Id, value: Value) {
        let kind = value.kind();
        self.data
            .entry(key)
            .or_default()
            .entry(kind)
            .or_default()
            .insert(value);
    }

    /// Get all values of a certain kind for a key.
    fn get_all(&self, key: &Id, kind: &Kind) -> Option<&IndexSet<Value>> {
        self.data.get(key).and_then(|kinds| kinds.get(kind))
    }
}

Routing implementation

Now it looks like we have run out of simple things to do and need to actually implement the routing part. The routing API does not care how the routing table is organized internally - it could just as well be the full set of nodes. But we want to implement the kademlia algorithm to get that nice power law distribution.

So let's define the routing table. First of all we need some simple integer arithmetic like xor and leading_zeros for 256 bit numbers. There are various crates that provide this, but since we don't need anything fancy like multiplication or division, we just quickly implemented it inline.

The routing table itself is just a 2d array of node ids. Each row (k-bucket) has a small fixed upper size, so we are going to use the ArrayVec crate to prevent allocations. For each node id we just keep a tiny bit of extra information - a timestamp when we have last seen any evidence that the node actually exists and responds, to decide which nodes to check for liveness.

A KBucket is tiny, so doing full scans for addition and removal is totally acceptable. We don't want any clever algorithms here.

struct NodeInfo {
    pub id: NodeId,
    pub last_seen: u64,
}

struct KBucket {
    nodes: ArrayVec<NodeInfo, 20>,
}

The routing table data is now just one bucket per bit, so 256 buckets in our case where we have decided to bucket by leading zero bits:

struct Buckets([KBucket; 256]);

The only additional information we need for the routing table is our own node id. Data in the routing table is organized in terms of closeness to the local node id, so we frequently need to access the local node id when inserting data.

struct RoutingTable {
    buckets: Box<Buckets>,
    local_id: NodeId,
}

Now assuming that the system has some way to find valid DHT nodes, all we need is a way to insert nodes into the routing table, and to query the routing table for the k closest nodes to some key x to implement the FindNode rpc call.

Insertion

Insertion means first computing which bucket the node should go into, and then inserting at that index. Computing the bucket index is computing the xor distance to our own node id, then counting leading zeros and flipping the result around, since we want bucket 0 to contain the closest nodes and bucket 255 to contain the furthest away nodes as per kademlia convention.

fn bucket_index(&self, target: &[u8; 32]) -> usize {
    let distance = xor(&self.local_id.as_bytes(), target);
    let zeros = leading_zeros(&distance);
    if zeros >= BUCKET_COUNT {
        0 // Same node case
    } else {
        BUCKET_COUNT - 1 - zeros
    }
}

fn add_node(&mut self, node: NodeInfo) -> bool {
    if node.id == self.local_id {
        return false;
    }

    let bucket_idx = self.bucket_index(node.id.as_bytes());
    self.buckets[bucket_idx].add_node(node)
}

Insertion in a bucket where the node already exists means just updating the timestamp. Otherwise just append the node, and if there is no room either make room by evicting the oldest existing node, or ping the oldest node and fail the insertion if the old node responds. For now we just fail, favoring stability. Nodes will be pinged in regular intervals anyway, and nodes that are non-responsive will be purged.

impl KBucket {
    fn add_node(&mut self, node: NodeInfo) -> bool {
        // Check if node already exists and update it
        for existing in &mut self.nodes {
            if existing.id == node.id {
                existing.last_seen = node.last_seen;
                return true; // Updated existing node
            }
        }

        // Add new node if space available
        if self.nodes.len() < K {
            self.nodes.push(node);
            return true;
        }

        false // Bucket full
    }
}

As you can see this is a very simple implementation. Within the bucket we don't care about order.

Querying

Since the xor metric is so simple, and the routing table is of limited size, it is not worth doing anything fancy when querying for a key. Conceptually we just create an array of nodes and distances, sort it by distance, take the k smallest, and that's it.

Since this operation is performed very frequently we did a few simple optimizations though.

impl RoutingTable {
    find_closest_nodes(&self, target: &Id, k: usize) -> Vec<NodeId> {
        let mut candidates = Vec::with_capacity(self.nodes().count());
        candidates.extend(
            self.nodes()
                .map(|node| Distance::between(target, node.id.as_bytes())),
        );
        if k < candidates.len() {
            candidates.select_nth_unstable(k - 1);
            candidates.truncate(k);
        }
        candidates.sort_unstable();

        candidates
            .into_iter()
            .map(|dist| {
                NodeId::from_bytes(&dist.inverse(target))
                    .expect("inverse called with different target than between")
            })
            .collect()
    }
}

We first create an array of candidates that contains all node ids in the routing table. This will almost always be larger than k.

We could just sort it, but we are only interested in the order of the k smallest values, not the overall order. So we can save some comparisons by using select_nth_unstable to sort such that the kth element is in the right place, then truncate and sort just the remaining <= k elements. We can always use unstable sort since the xor distance is an injective function, no two nodes can have the same distance to target id.

As a last trick, instead of storing (id, distance) tuples we just store the distance itself while sorting, and recompute the node id itself by xor-ing again with the target id. This reduces the size of the temporary array by half.

Wiring it up

The handler for our rpc protocol is a typical rust actor. The actor has the mem storage as well as the routing table as state, and processes messages one by one. If the storage was persistent, you might want to perform the actual storage and retrieval as well as the sending of the response stream in a background task, but for now it is all sequential.

There are some background tasks to update the routing table to add new nodes and forget unreachable nodes, but these are omitted for now.

struct Node {
    routing_table: RoutingTable,
    storage: MemStorage,
}

struct Actor {
    node: Node,
    /// receiver for rpc messages from the network
    rpc_rx: tokio::sync::mpsc::Receiver<RpcMessage>,
    ... more plumbing for background tasks
}

impl Actor {
    async fn run(mut self) {
        loop {
            tokio::select! {
                msg = self.rpc_rx.recv() => {
                    if let Some(msg) = msg {
                        self.handle_rpc(msg).await;
                    } else {
                        break;
                    }
                }
                ... other background tasks and stuff
            }
        }
    }

    async fn handle_rpc(&mut self, message: RpcMessage) {
        match message {
            RpcMessage::Set(msg) => {
                /// msg validation omitted
                self.node.storage.set(msg.key, msg.value.clone());
                msg.tx.send(SetResponse::Ok).await.ok();
            }
            RpcMessage::GetAll(msg) => {
                let Some(values) = self.node.storage.get_all(&msg.key, &msg.kind) else {
                    return;
                };
                // sampling values and randomizing omitted
                for value in values {
                    if msg.tx.send(value.clone()).await.is_err() {
                        break;
                    }
                }
            }
            RpcMessage::FindNode(msg) => {
                // call local find_node and just return the results
                let ids = self
                    .node
                    .routing_table
                    .find_closest_nodes(&msg.id, self.state.config.k)
                    .into_iter()
                    .map(|id| self.state.pool.node_addr(id))
                    .collect();
                msg.tx.send(ids).await.ok();
            }
        }
    }
}

Set is trivial. It just sets the value and returns Ok to the requester. There is some logic to validate the value based on the key, but this has been omitted here.

GetAll is a bit more complex. It queries the storage for values, then does some limiting and randomizing (omitted here), and the streams out the responses.

FindNode queries the routing table and gets back a sequence of node ids. It then augments this information with dialing information from the connection pool (a wrapper around an iroh endpoint) and sends out the response all at once.

What we have now is an actor that stores values and maintains a routing table. All rpc operations are fully local, there is no way for a remote node to trigger something expensive.

The next step is to implement the iterative lookup algorithm. Once we have that, storage and retrieval are just calls to the k closest nodes to a key that are the result of the iterative lookup algorithm.

Both storage and retrieval involve a lot of network operations. To hide all these details from the user, we will need a message based protocol that the DHT client uses to communicate with the DHT actor. This will also be an irpc protocol, but it will be used either in memory or to control a DHT node running in a different process on a local machine, so it does not have to concern itself as much with having small messages and with adversarial scenarios.

We also don't have to care about stability, since this will be used only between the same version of the binary.

As mentined, the main complexity of a DHT is the routing. What values we store almost does not matter, as long as they can be validated somehow and are small enough to fit. So for testing, we are going to implement just storage of immutable small blobs.

We need the ability to store and retrieve such blobs, and for the user facing API we don't care about nodes. All these details are for the DHT to sort out internally. So let's design the API.

The API protocol will also contain internal messages that the DHT needs for periodic tasks. We can just hide them from the public API wrapper if we don't want our users to mess with internals.

#[rpc_requests(message = ApiMessage)]
#[derive(Debug, Serialize, Deserialize)]
pub enum ApiProto {
    #[rpc(wrap, tx = mpsc::Sender<NodeId>)]
    NetworkPut { id: Id, value: Value },
    #[rpc(wrap, tx = mpsc::Sender<(NodeId, Value)>)]
    NetworkGet { id: Id, kind: Kind },
    ... plumbing rpc calls
}

We need the ability to store and retrieve values.

Storing values is a two step process, first use the iterative algorithm to find the k closest nodes, then, in parallel, try to store the value on all these nodes. To give the user some feedback over where the data is stored, we return a stream of node ids where the data was successfully stored.

Retrieval is almost identical. We first find the k closest nodes, then, in parallel, ask all of them for the value. Again we return a stream of (NodeId, Value) so we can get answers to the user as soon as they become available.

In case of immutable values, the first validated value is all it takes, as soon as we got that we can abort the operation. For other values we might want to wait for all results and then choose the most recent one, or use them all, e.g. to retrieve content over iroh-blobs from multiple sources.

Here is the ApiClient for the get_immutable and put_immutable rpc calls:

async fn put_immutable(
    &self,
    value: &[u8],
) -> irpc::Result<(blake3::Hash, Vec<NodeId>)> {
    let hash = blake3::hash(value);
    let id = Id::from(*hash.as_bytes());
    let mut rx = self
        .0
        .server_streaming(
            NetworkPut {
                id,
                value: Value::Blake3Immutable(Blake3Immutable {
                    timestamp: now(),
                    data: value.to_vec(),
                }),
            },
            32,
        )
        .await?;
    let mut res = Vec::new();
    loop {
        match rx.recv().await {
            Ok(Some(id)) => res.push(id),
            Ok(None) => break,
            Err(_) => {}
        }
    }
    Ok((hash, res))
}

async fn get_immutable(&self, hash: blake3::Hash) -> irpc::Result<Option<Vec<u8>>> {
    let id = Id::from(*hash.as_bytes());
    let mut rx = self
        .0
        .server_streaming(
            NetworkGet {
                id,
                kind: Kind::Blake3Immutable,
            },
            32,
        )
        .await?;
    loop {
        match rx.recv().await {
            Ok(Some((_, value))) => {
                let Value::Blake3Immutable(Blake3Immutable { data, .. }) = value else {
                    continue; // Skip non-Blake3Immutable values
                };
                if blake3::hash(&data) == hash {
                    return Ok(Some(data));
                } else {
                    continue; // Hash mismatch, skip this value
                }
            }
            Ok(None) => {
                break Ok(None);
            }
            Err(e) => {
                break Err(e.into());
            }
        }
    }
}

put_immutable aggregates all node ids where the data was stored and returns them. You could have a different API where you don't wait for storage on all nodes. get_immutable just returns after the first correct value - at this point you have the correct data and there is no point in waiting for more of the same.

The first phase of the implementation of both NetworkPut and NetworkGet is powered by the iterative lookup algo. Since this is used both externally to store and retrieve values and internally to perform random lookups to maintain the routing table, it gets its own RPC call.

pub enum ApiProto {
    ...
    #[rpc(wrap, tx = oneshot::Sender<Vec<NodeId>>)]
    Lookup {
        initial: Option<Vec<NodeId>>,
        id: Id,
    },
    ...
}
...
impl ApiClient {
    async fn lookup(
        &self,
        id: Id,
        initial: Option<Vec<NodeId>>,
    ) -> irpc::Result<Vec<NodeId>> {
        self.0.rpc(Lookup { id, initial }).await
    }
}

Lookup gets an initial set of node ids to start, and an id to look up. It returns the k closest nodes to the id. All the internals of the iterative lookup algorithm are hidden.

The plumbing to process this is not that interesting. But let's take a look at the iterative lookup algorithm itself now:

async fn iterative_find_node(self, target: Id, initial: Vec<NodeId>) -> Vec<NodeId> {
    let mut candidates = initial
        .into_iter()
        .filter(|addr| *addr != self.pool.id())
        .map(|id| (Distance::between(&target, &id.as_bytes()), id))
        .collect::<BTreeSet<_>>();
    let mut queried = HashSet::new();
    let mut tasks = FuturesUnordered::new();
    let mut result = BTreeSet::new();
    queried.insert(self.pool.id());
    result.insert((
        Distance::between(&self.pool.id().as_bytes(), &target),
        self.pool.id(),
    ));

    loop {
        for _ in 0..self.config.alpha {
            let Some(pair @ (_, id)) = candidates.pop_first() else {
                break;
            };
            queried.insert(id);
            let fut = self.query_one(id, target);
            tasks.push(async move { (pair, fut.await) });
        }

        while let Some((pair @ (_, id), cands)) = tasks.next().await {
            let Ok(cands) = cands else {
                self.api.nodes_dead(&[id]).await.ok();
                continue;
            };
            for cand in cands {
                let dist = Distance::between(&target, &cand.as_bytes());
                if !queried.contains(&cand) {
                    candidates.insert((dist, cand));
                }
            }
            self.api.nodes_seen(&[id]).await.ok();
            result.insert(pair);
        }

        // truncate the result to k.
        while result.len() > self.config.k {
            result.pop_last();
        }

        // find the k-th best distance
        let kth_best_distance = result
            .iter()
            .nth(self.config.k - 1)
            .map(|(dist, _)| *dist)
            .unwrap_or(Distance::MAX);

        // true if we candidates that are better than distance for result[k-1].
        let has_closer_candidates = candidates
            .first()
            .map(|(dist, _)| *dist < kth_best_distance)
            .unwrap_or_default();

        if !has_closer_candidates {
            break;
        }
    }

    // result already has size <= k
    result.into_iter().map(|(_, id)| id).collect()
}

The algorithm maintains a set of candidates sorted by distance to the target. This set is initially populated from the local routing table, or can be passed in by the user.

It also maintains a set of nodes that were already queried to prevent running around in circles. The id of the node itself is added to the queried set to prevent self queries. It is also added to the result set for the case where the node itself is in the set of closest nodes.

Last but not least, it maintains a set of result nodes sorted by distance to the target. The only way for a node to end up in the result set is if it has actually answered a query, so is proven to be alive from the point of view of the local node at the time of the query.

The algorithm makes no assumptions whatsoever about the candidates, not even that they exist. So it pulls candidates in distance order with a configurable parallelism level alpha and validates them by performing a FindNode query on them for the target key. Ongoing FindNode queries are tracked in a FuturesUnordered.

As FindNode tasks complete, we get information about whether the candidate is alive or not.

For unreachable candidates, we drop them but also inform the actor that the node id should be removed from the routing table. For reachable nodes, we add the node we called to the result and the nodes the node returned to the candidates set. We can't add them to the result yet since they might be stale, or the node might lie to us. We also call nodes_seen to update the timestamp of the node in the routing table.

We only ever keep the best k nodes in the result set. The abort criterion is the most tricky part. We want to abort if none of the candidates is better than the kth best node in the result set, or if we have run out of candidates to try.

There might be an off by one error somewhere in there, but the algorithm seems to work well. The algorithm does not do any pings to check node liveness, since a Ping request and a FindNode request are identical in terms of latency and cost, and a FindNode request does something useful.

NetworkGet and NetworkPut

The iterative lookup algorithm is really the most complex part, but for completeness sake here is how the actual NetworkGet and NetworkPut rpc calls are implemented. We first get good initial candidates from the local routing table. Even a pure client node will after some time accumulate some knowledge about the network that is useful for finding good places to start the search.

async fn handle_api(&mut self, message: ApiMessage) {
    match message {
        ...
        ApiMessage::NetworkGet(msg) => {
            let initial = self.node.routing_table.find_closest_nodes(&msg.id, K);
            self.tasks.spawn(self.state.clone().network_get(initial, msg.inner, msg.tx));
        }
        ...
    }
}

The network_get itself, which is run in a task, then just calls the iterative_find_node fn above to find the k closest nodes, and then attempts to get the value from all of them with a configurable parallelism level, returning results to the caller immediately as they arrive.

The network_put fn looks extremely similar.

async fn network_get(
    self,
    initial: Vec<NodeId>,
    msg: NetworkGet,
    tx: mpsc::Sender<(NodeId, Value)>,
) {
    let ids = self.clone().iterative_find_node(msg.id, initial).await;
    stream::iter(ids)
        .for_each_concurrent(self.config.parallelism, |id| {
            let pool = self.pool.clone();
            let tx = tx.clone();
            let msg = NetworkGet { id: msg.id, kind: msg.kind };
            async move {
                let Ok(client) = pool.client(id).await else {
                    return;
                };
                // Get all values of the specified kind for the key
                let Ok(mut rx) = client.get_all(msg.id, msg.kind).await else {
                    return;
                };
                while let Ok(Some(value)) = rx.recv().await {
                    if tx.send((id, value)).await.is_err() {
                        break;
                    }
                }
                drop(client);
            }
        })
        .await;
}

Does this work?

Ok, now it seems that we have written a rudimentary DHT. There are some missing parts, such as routing table maintenance. Every query will update the routing table by calling nodes_seen or nodes_dead, but we also want to actively maintain the routing table even if there are no user queries.

But before we get lost in these details... Does this thing even work? Sure, we can write unit tests for the various components such as the routing table. But that won't tell us all that much about the behaviour of a system of thousands of nodes.

What we need is a realistically sized DHT that we can just prod by storing values and see if it behaves correctly. Ideally we want to be able to do this without setting up a kubernetes cluster of actual machines. For the behaviour of the algorithm in the happy case it is sufficient to just simulate a lot of DHT nodes in memory in a single process, connected via irpc memory channels.

For a slightly more realistic simulation we can create a large number of actual DHT nodes that communicate via iroh connections. This can still all happen within a single process, but will be more expensive.

Taking a step back, what does it mean for a DHT to work anyway? Sure, we can put values in and get them out again. But there are various pathological cases where the DHT will seem to work but really does not.

E.g. the DHT could decide to store all values on one node, which works just fine but completely defeats the purpose of a DHT. Or it could only work for certain keys.

So we need to take a look at the DHT node internals and see if it works in the expected way.

Validating lookups

As we have seen, the iterative algorithm to find the k closest nodes is at the core of the DHT. Fortunately, for a test scenario we know the perfect result of that call. We can just take the entire set of node ids we have set up for the test, compute the k closest to the target node, and compare this set with the set returned by lookup/iterative_find_node. The intersection between the set returned by lookup and the perfect set of node ids gives us a somewhat more precise way to measure the quality of the routing algorithm. For a fully initialized DHT it should be almost always perfect overlap.

Almost, because the algorithm is random and greedy, and there is always a tiny chance that a node can not be found.

We need to perform this test for a large number of randomly chosen keys to prevent being fooled by a DHT that only works for certain values.

Validating data distribution

A perfect overlap with the perfect set does not mean that everything is perfect. E.g. we could have a bug in our metric that leads to always the 20 smallest nodes in the set being chosen. Both the brute force scan and the iterative lookup would always find these 20 nodes, but data would not be evenly distributed across the network, which defeats the whole purpose of a DHT.

So another useful test is to store a number of random values and check the data distribution in the DHT. Data should be evenly distributed around all nodes, with just the inevitable statistical variation.

Visualizing the results

In all these cases, we are going to get a lot of data, and the results are not precise enough to be checked in classical unit tests. Instead we are going to plot things like overlap with the perfect set of node ids as well as data distribution, and to condense the information even further plot histograms of these distributions.

Later it would be valuable to compute statitical properties of the distributions and check them against expectations. But for now we just need some basic way to check if the thing works at all. So let's write some tests...

Testing in memory with irpc

One of the plumbing details we omitted when describing the inner workings of the DHT actor is the client pool. A DHT node is doing a lot of tiny interactions with a lot of nodes, so we don't want to open a connection every time we talk to a remote node. But we also don't want to keep connections open indefinitely, since there will be a lot of them. So one of the things the DHT actor has is an abstract client pool that can provide a client given a remote node id.

pub trait ClientPool: Send + Sync + Clone + Sized + 'static {
    /// Our own node id
    fn id(&self) -> NodeId;

    /// Adds dialing info to a node id.
    ///
    /// The default impl doesn't add anything.
    fn node_addr(&self, node_id: NodeId) -> NodeAddr {
        node_id.into()
    }

    /// Adds dialing info for a node id.
    ///
    /// The default impl doesn't add anything.
    fn add_node_addr(&self, _addr: NodeAddr) {}

    /// Use the client to perform an operation.
    ///
    /// You must not clone the client out of the closure. If you do, this client
    /// can become unusable at any time!
    fn client(&self, id: NodeId) -> impl Future<Output = Result<RpcClient, String>> + Send;
}

The client pool is used inside the DHT actor whenever it needs to talk to a remote client. It has ways to add and retrieve dialing information for node ids, but most importantly a way to get a RpcClient. This client can be backed either by an actual iroh connection, or just an extremely cheap tokio mpsc channel.

For testing, we are going to implement a TestPool that just holds a set of memory clients that is populated during test setup.

#[derive(Debug, Clone)]
struct TestPool {
    clients: Arc<Mutex<BTreeMap<NodeId, RpcClient>>>,
    node_id: NodeId,
}

impl ClientPool for TestPool {
    async fn client(&self, id: NodeId) -> Result<RpcClient, String> {
        let client = self
            .clients
            .lock()
            .unwrap()
            .get(&id)
            .cloned()
            .ok_or_else(|| format!("client not found: {}", id))?;
        Ok(client)
    }

    fn id(&self) -> NodeId {
        self.node_id
    }
}

Each DHT node gets their own TestPool, but they all share the map from NodeId to RpcClient. So this is extremely cheap.

Tests with perfect routing tables

The first test we can perform is to give all nodes perfect¹ knowledge about the network by just telling them about all other node ids, then perform storage and queries and look at statistics. If there is something fundamentally wrong with the routing algorithm we should see it here. At this point tests are just printing output, so they need to be run with --nocapture.

We are using the textplots crate to get nice plots in the console, with some of the plotting code written by claude.

> cargo test perfect_routing_tables_1k -- --nocapture

Histogram - Commonality with perfect set of 20 ids
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⢸⠉⠉⡇ 100.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁⠈⠁ 0.0
0.0                                           20.0

So far, so good. We get a 100% overlap with the perfect set of ids.

Storage usage per node
⡁⠈⢸⢹⠈⣿⣿⠈⠀⠁⠈⠀⠁⢸⢸⠁⠈⠀⠁⢸⢸⡇⠈⠀⠁⠈⢸⠁⠈⠀⠁⠈⠀⠁⢸⠀⠁⣿⢸⢹⡏⡇⠁⠈⠀⠁⠈⠀⠁⠈⡁ 8.0
⠄⠀⣾⢸⠀⣿⣿⠀⢰⠀⠀⠀⠀⢸⢸⠀⠀⢰⠀⢸⢸⡇⠀⠀⢰⠀⢸⠀⡆⢰⠀⠀⠀⠀⢸⡆⢰⣿⢸⣾⡇⡇⠀⠀⠀⠀⠀⢰⠀⢰⠄
⠂⠀⣿⢸⠀⣿⣿⢠⢸⠀⠀⠀⠀⣼⣼⠀⠀⢸⠀⢸⢸⡇⢠⢠⣼⠀⢸⠀⡇⢸⠀⠀⠀⢠⢸⡇⢸⣿⢸⣿⣧⡇⡄⠀⠀⠀⠀⢸⠀⢸⠂
⣁⠀⣿⢸⢀⣿⣿⢸⢸⡀⢀⠀⠀⣿⣿⠀⢀⢸⠀⢸⣸⡇⢸⢸⣿⡀⢸⣀⡇⢸⠀⢀⠀⣸⢸⣇⢸⣿⢸⣿⣿⣇⡇⢀⢀⣀⡀⢸⠀⣸⡁
⢼⠀⣿⢸⢸⣿⣿⢸⢸⡇⢸⠀⠀⣿⣿⠀⢸⢸⠀⢸⣿⡇⢸⢸⣿⡇⢸⣿⡇⢸⠀⢸⠀⣿⢸⣿⢸⣿⢸⣿⣿⣿⡇⢸⢸⣿⡇⢸⠀⣿⠄
⢺⣿⣿⢸⣿⣿⣿⣿⣿⣿⣿⠀⣿⣿⣿⣿⢸⢸⠀⣿⣿⣿⣿⣿⣿⣿⢸⣿⡇⣿⢸⣿⣿⣿⣿⣿⢸⣿⣿⣿⣿⣿⡇⣿⣿⣿⣿⣿⡇⣿⡇
⣿⣿⣿⣾⣿⣿⣿⣿⣿⣿⣿⣶⣿⣿⣿⣿⣾⣾⡆⣿⣿⣿⣿⣿⣿⣿⣾⣿⣷⣿⣾⣿⣿⣿⣿⣿⣾⣿⣿⣿⣿⣿⣷⣿⣿⣿⣿⣿⣷⣿⡇
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣧⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁ 0.0
0.0                                          999.0

Histogram - Storage usage per node
⡏⠉⠉⠉⠉⠉⢹⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⡁ 310.0
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⡇⠀⠀⠀⠀⠀⢸⠉⠉⠉⠉⠉⢹⣀⣀⣀⣀⣀⣀⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⡏⠉⠉⠉⠉⠉⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡇⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⡧⠤⠤⠤⠤⠤⢤⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣀⣀⣀⣀⣀⡁
⠁⠈⠀⠁⠈⠀⠉⠈⠀⠁⠈⠀⠉⠈⠀⠁⠈⠀⠁⠉⠀⠁⠈⠀⠁⠉⠀⠁⠈⠀⠁⠈⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁⠁⠈⠀⠁⠈⠁ 14.0
0.0                                            8.0

Data is evenly distributed over the DHT nodes. The histogram also looks reasonable. Since we have 100% overlap with the perfect set of nodes, the little bump at the end is just a blip, provided or XOR metric works.

Routing table size per node
⣹⣯⡇⢡⡌⡇⠁⠈⡇⠁⠈⣿⡅⣼⢠⠁⠈⢠⠁⠈⢠⡇⣯⠀⢹⣿⢠⠁⠈⠀⡇⠈⠀⠁⠈⡇⠁⠈⣤⣽⢨⠀⠁⡌⠀⢹⣿⢸⣿⢸⡁ 141.0
⢼⣿⣿⢸⣿⡇⡇⣿⡇⢸⡇⣿⣿⣿⢸⡇⢸⣿⡇⠀⣿⣿⣿⡇⢸⣿⢸⣿⠀⠀⣿⣿⡇⢸⣿⣿⣿⡇⣿⣿⣿⢸⣿⣿⠀⣿⣿⢸⣿⢸⠄
⣺⣿⣿⣿⣿⣧⣇⣿⡇⣸⣿⣿⣿⣿⣿⣧⢸⣿⣿⠀⣿⣿⣿⣿⣸⣿⣿⣿⣧⡀⣿⣿⣿⣸⣿⣿⣿⡇⣿⣿⣿⣿⣿⣿⢸⣿⣿⣿⣿⣼⠂
⣿⣿⣿⣿⣿⣿⣿⣿⣇⣿⣿⣿⣿⣿⣿⣿⣸⣿⣿⣶⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣿⣿⣿⣿⣿⣿⣿⣷⣿⣿⣿⣿⣿⣿⣾⣿⣿⣿⣿⣿⡁
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡄
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁ 120.0
0.0                                          999.0

Histogram - Routing table size per node
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⢸⡇⠁⠈⡁ 186.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⡇⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⡇⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⡇⠀⠀⡁
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⡇⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢀⠀⢸⡇⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⢀⢸⣿⡇⣤⡁
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣴⣾⣿⣸⣿⣇⣿⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⡂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⡇
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁ 0.0
0.0                                          141.0

All routing tables have roughly the same size. Not surprising since we have initialized them all with a randomized sequence of all node ids.

Tests with almost empty routing tables

But the above just tells us that the DHT works if we initialize the routing tables with all node ids. That is not how it works in the real world. Nodes come and go, and the DHT is supposed to learn about the network.

So let's write a test where we initially don't have perfect routing information.

We need to give each node at least some initial information about the rest of the network, so we arrange the nodes in a ring and give each node the next 20 nodes in the ring as initial nodes in their routing table (bootstrap nodes). We know that in principle every node is connected with every other node this way, but we also know that this is not going to lead to perfect routing.

So let's see how bad it is.

❯ cargo test just_bootstrap_1k -- --nocapture

Histogram - Commonality with perfect set of 20 ids
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⢸⠉⠉⠉⠉⡇⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⡁ 22.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⣀⣀⣀⣀⣸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⠄⠀⠀⠀⢀⣀⣀⣀⣀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢀⣀⣀⣀⣀⣀⣀⣀⣀⣀⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⡖⠒⠒⠒⢺⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡗⠒⠒⠒⢺⠀⠀⠀⠀⢸⠀⠀⠀⠀⡗⠒⠒⠒⢲⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡏⠉⠉⠉⢹⠀⠀⠀⠀⠂
⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠤⠤⠤⠤⡇⠀⠀⠀⢸⠀⠀⠀⠀⡁
⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠉⠈⠀⠁⠈⠁⠁⠈⠀⠉⠈⠀⠁⠈⠁⠁⠈⠀⠉⠉⠉⠉⠉⠁ 1.0
0.0                                           11.0

Pretty bad. The routing gives between 0 and 11 correct nodes. Note that even with this very suboptimal routing table setup the lookup would work 100% of the time if you use the same node for storage and retrieval, since it always gives the same wrong answer. If you were to use different nodes, there is still some decent chance of an overlap.

Let's look at more stats:

Storage usage per node
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⢸⢠⢡⠈⡄⠁⡏⢸⣧⡏⠀⢹⡏⡇⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⡁ 17.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⢸⢸⡆⣷⠀⣇⣸⣿⣇⠀⢸⣇⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣾⢸⣾⣷⣿⠀⣿⣿⣿⣿⠀⢸⣿⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣤⢸⣿⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⠀⢀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣶⣾⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢸⣿⡇⠀⠀⠀⠀⠀⠀⡁
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢸⣿⡇⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣾⣿⡇⡀⡆⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⣧⣧⢠⠀⠀⠀⡁
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁ 0.0
0.0                                          999.0

We interact with the node with index 500, and since each node only knows about nodes further right on the ring, the nodes to the left of our initial node are not used at all.

Routing table size per node
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⡏⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⡁ 90.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁ 20.0
0.0                                          999.0

We have only interacted with node 500, so it has learned a bit about the network. But the other nodes only have the initial 20 bootstrap nodes. We have run all nodes in transient mode, so they don't learn about other nodes unless they actively perform a query, which in this case only node 500 has done.

Testing active routing table maintenance

An important part of a DHT node is active routing table maintenance to learn about other nodes proactively. Here is a test where each node performs a lookup of its own node id in periodic intervals just to learn about the rest of the world.

cargo test --release self_lookup_strategy -- --nocapture

Initially things look just as bad as with just bootstrap nodes:

Histogram - Commonality with perfect set of 20 ids
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⢸⠉⠉⠉⠉⡇⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⡁ 23.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⡖⠒⠒⠒⢺⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⠄⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⢠⠤⠤⠤⠤⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠉⠉⠉⠉⢹⠉⠉⠉⠉⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⡖⠒⠒⠒⢺⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡗⠒⠒⠒⢺⠀⠀⠀⠀⢸⠀⠀⠀⠀⡗⠒⠒⠒⢲⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡖⠒⠒⠒⢲⠀⠀⠀⠀⠂
⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠀⠀⠀⠀⢸⠀⠀⠀⠀⡇⠀⠀⠀⢸⠤⠤⠤⠤⡇⠀⠀⠀⢸⠀⠀⠀⠀⡁
⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠉⠈⠀⠁⠈⠁⠁⠈⠀⠉⠈⠀⠁⠈⠁⠁⠈⠀⠉⠉⠉⠉⠉⠁ 1.0
0.0                                           11.0

But after just a few random lookups, routing results are perfect for this small DHT

Histogram - Commonality with perfect set of 20 ids
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⢸⠉⠉⡇ 96.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⢸⠀⠀⡇
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡤⠤⢼⠀⠀⡇
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁⠈⠈⠁⠈⠁ 0.0
0.0                                           20.0

The node that is being probed can still be clearly seen, but after just a few self lookups at least all nodes have reasonably sized routing tables:

Routing table size per node
⡁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⡏⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⠀⠁⠈⡁ 131.0
⠄⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⡁⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⠄⠀⠀⠀⠀⠀⠀⠀⢀⡀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠄
⠂⠀⠀⠀⠀⠀⠀⠀⢸⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠂
⣵⡆⢀⠀⠀⡀⠀⢀⢸⡇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣇⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⡁
⣿⣿⣾⣠⣆⣧⣦⣾⣾⡇⠀⡀⠀⣸⠀⡄⢀⠀⠀⠀⢰⡀⠀⣀⣀⣿⣼⣼⣦⣀⠀⠀⠀⠀⠀⠀⠀⢀⢀⣷⣶⡆⣤⣄⢠⡀⠀⠀⠀⠀⠄
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣴⣧⣾⣿⣿⣿⣾⣼⣆⣧⣿⣷⣸⣿⣿⣿⣿⣿⣿⣿⣇⣀⣼⣸⣴⣤⣿⣼⣿⣿⣿⣿⣿⣿⣿⣧⡀⠀⡄⣀⡂
⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇
⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠉⠁ 42.0
0.0                                          999.0

How big can you go?

With the memory based tests you can easily go up to 10k nodes, and even go up to 100k nodes with a lot of patience, on a 32GiB macbook pro. The limiting factor is the fixed size of the routing table. For a 100k node test, just the routing tables alone are ~20 GiB. You could optimize this even further by having a more compact routing table or my memoizing/Arc-ing node ids, but this would come with downsides for performance in production, and in any case 100k nodes already is a lot.

An evolving network

So now we have tests to show that the routing works as designed when the routing tables are properly initialized, and also tests that the routing table maintenance strategies work to properly initiailze the routing tables over time.

What is missing is to simulate a more dynamic network where nodes come and go. We need to know if routing tables eventually learn about new nodes and forget about dead nodes. These kinds of tests don't benefit from running over real iroh connections, so we are going to use mem connections.

Nodes joining

Having a static test setup with a fixed number of nodes is nice and simple. So we have to set things up such that we still have n nodes, but some are initially disconnected. Then do something to connect them to the rest and watch the system evolve. The key for this is the set of bootstrap nodes. We can set up some nodes without bootstrap nodes, and make sure the set of bootstrap nodes for the connected nodes does not contain any of the partitioned nodes. The partitioned nodes will be completely invisible from the connected nodes, as if they don't exist at all.

Then, after some time, do something to connect the disconnected nodes, e.g. tell each of them about one node in the connected set. That should be enough for them to eventually learn about the other nodes, and also for the other nodes to learn about them.

Let's look at the test setup:

async fn partition_1k() -> TestResult<()> {
    // all nodes have all the strategies enabled
    let config = Config::full();
    let n = 1000;
    let k = 900;
    let bootstrap = |i| {
        if i < k {
            // nodes below k form a ring
            (1..=20).map(|j| (i + j) % k).collect::<Vec<_>>()
        } else {
            // nodes above k don't have bootstrap peers
            vec![]
        }
    };
    let secrets = create_secrets(0, n);
    let ids = create_node_ids(&secrets);
    let (nodes, _clients) = create_nodes_and_clients(&ids, bootstrap, config).await;
    ...
}

We configure the nodes with all routing table maintenance strategies enabled. Then we create 900 nodes that are connected in a ring, and 100 nodes that don't have any bootstrap nodes (create_nodes_and_clients takes a function that gives the indices of the bootstrap node for each node).

Then we let the system run for some time so the 900 connected nodes have some time to learn about each other. Then comes the interesting part - we tell each of the 100 disconnected nodes about 1 of the 900 connected nodes.

    for _i in 0..10 {
        tokio::time::sleep(Duration::from_secs(1)).await;
        // visualize results
    }
    let id0 = nodes[0].0;
    // tell the partitioned nodes about id0
    for i in k..n {
        let (_, (_, api)) = &nodes[i];
        api.nodes_seen(&[id0]).await.ok();
    }
    for _i in 0..30 {
        tokio::time::sleep(Duration::from_secs(1)).await;
        // visualize results
    }

Now the 100 previously disconnected nodes should learn about the main swarm of 900 nodes, and more importantly the 900 nodes of the main swarm should learn about the 100 new nodes.

But how do we visualize results? First of all we need a way to show the state of the system at one point in time. We got 1000 nodes, so each node can have at most 1000 entries in its routing table. So we could have a bitmap of 1000 rows where each row is the routing table of that node.

But now we need to additionally show evolution of this bitmap over time. Fortunately there are great libraries for animated gifs in rust, so we can just generate an animated gif that shows the evolution of the connectivity map over time.

Here it is:

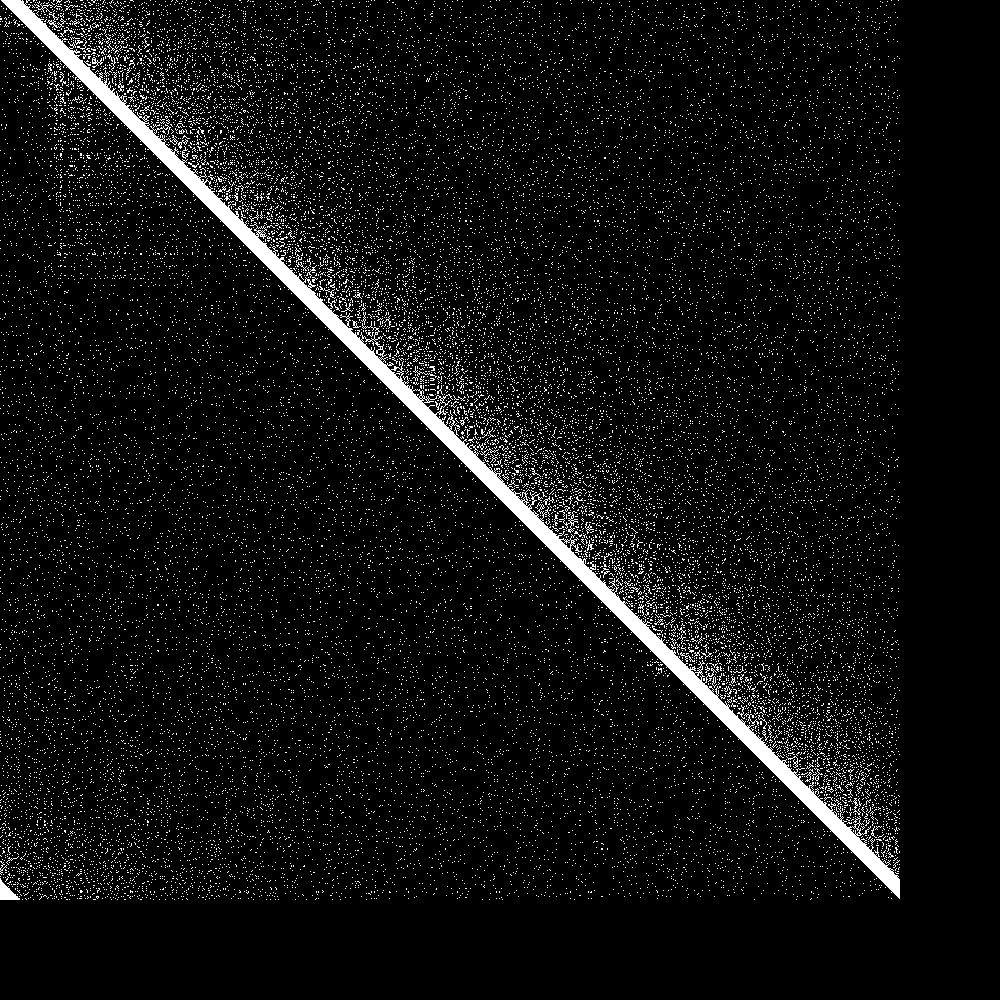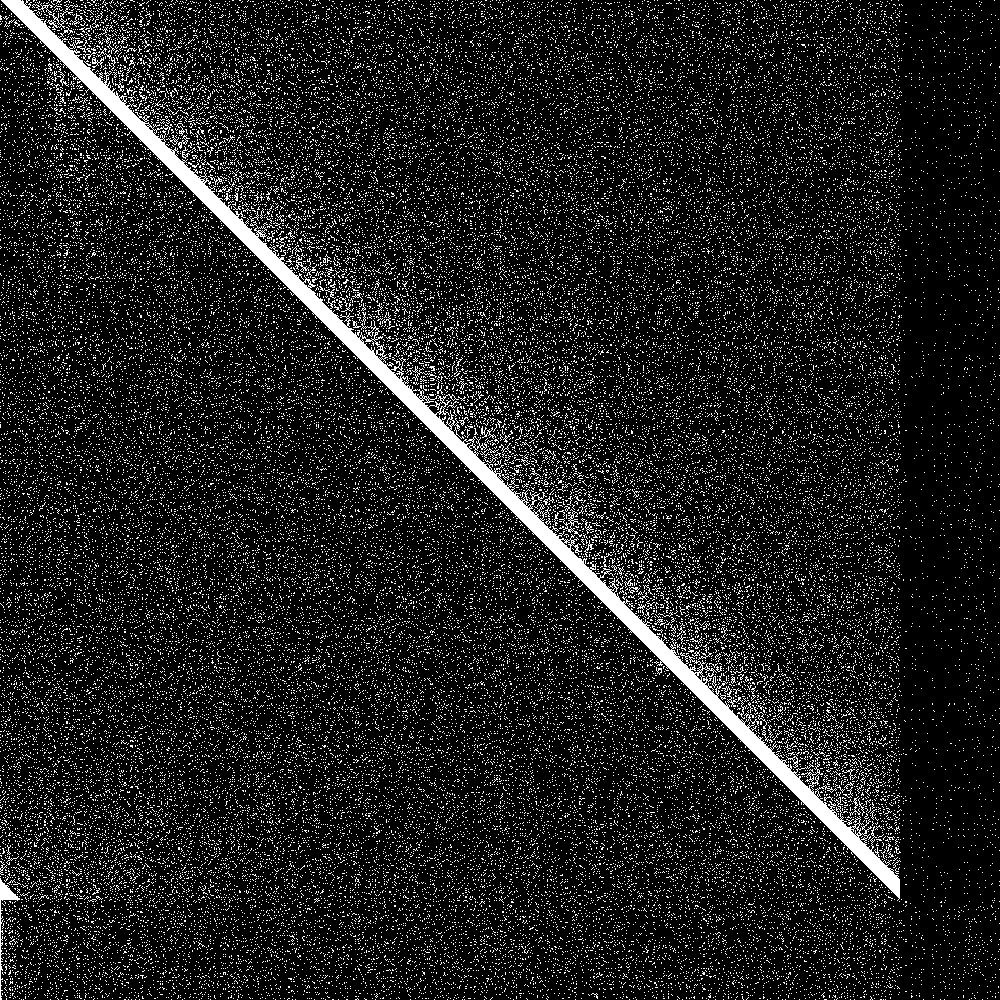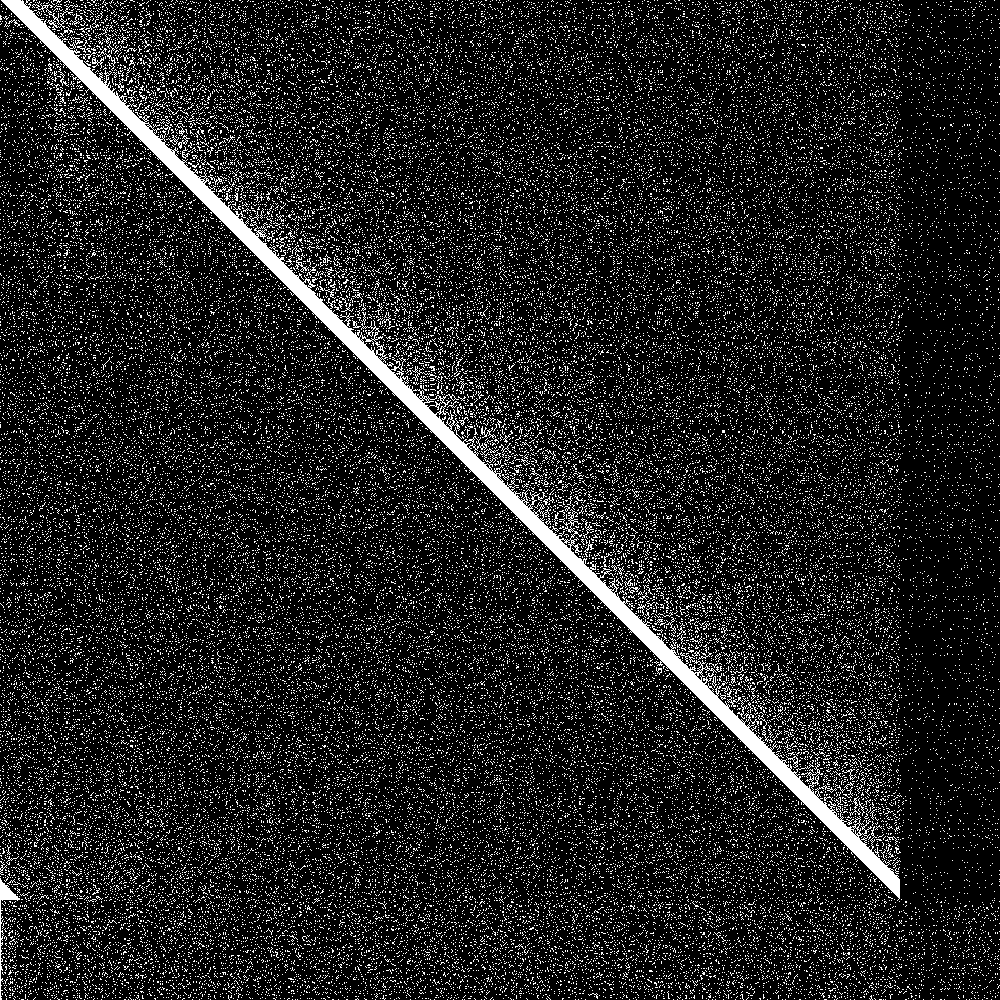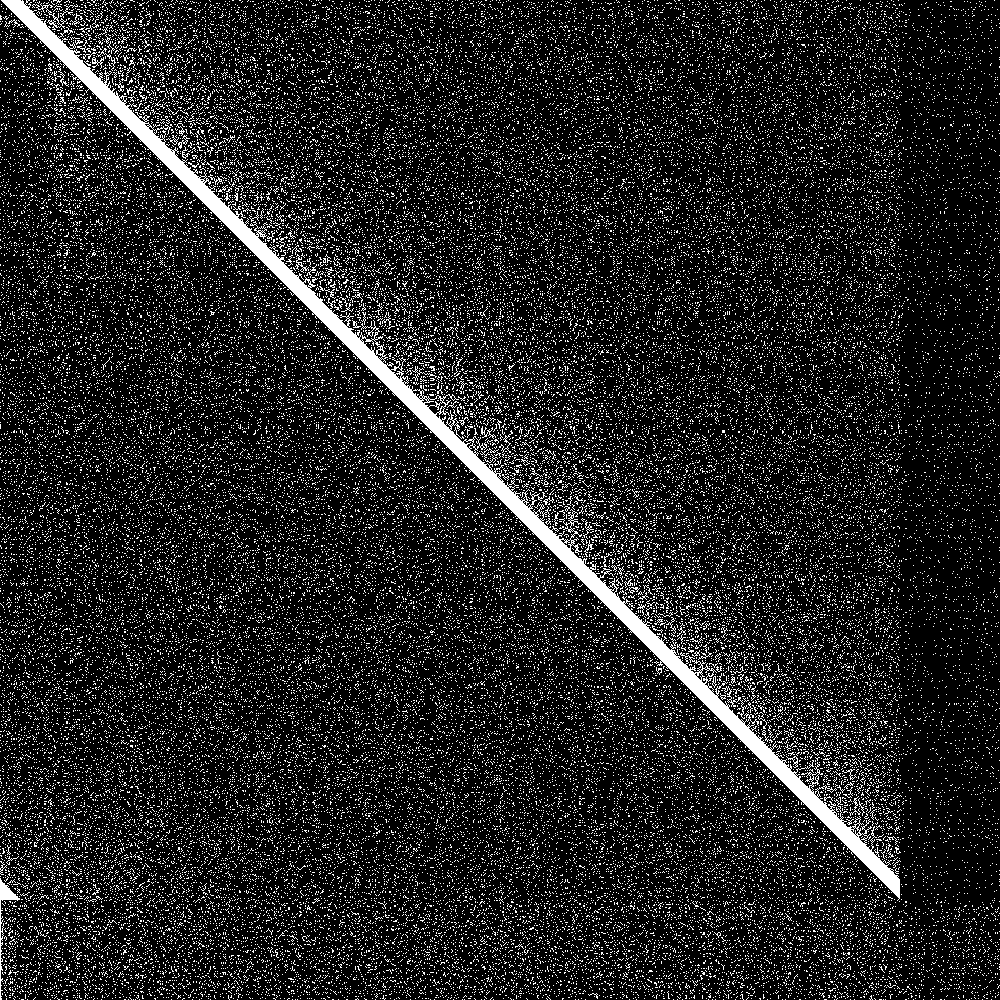
The big diagonal bar is the bootstrap nodes. As you can see they wrap around at 900. The lowest 100 rows are the routing tables of the initially disconnected nodes, and the rightmost 100 pixels is the knowledge of the connected nodes of the initially disconnected rows. Both are initially empty. As soon as the 100 partitioned nodes are connected, the 100 new nodes very quickly learn about the main swarm, and the main swarm somewhat more slowly learns about the 100 new nodes. So everything works as designed.

You could now experiment with different routing table maintenance strategies to make things faster. But fundamentally, things work already. After some time the 100 new nodes would be fully integrated into the swarm.

Nodes leaving

Another thing we need to test is nodes leaving. When nodes leave for whatever reason, the remaining nodes should notice and purge these nodes from their routing tables after some time. This is necessary for the DHT to continue functioning - a routing table full of dead nodes is worthless. We don't want to immediately forget about nodes when they are briefly unreachable - they might come back, but we should eventually get rid of them.

The way deleting dead nodes works in this DHT impl is also via random key lookups. If you notice during a key lookup that a node in your routing table is unreachable, you will purge it from the routing table briefly afterwards. So a node that has all the active routing table maintenance strategies enabled should also automatically get rid of dead nodes over time.

How do we test this? We have 1000 fully connected nodes like in many previous tests, then "kill" the last 100 of them and observe the evolution of the system. For our mem connection pool this is easy to do by just reaching into the underlying BTreeMap<NodeId, RpcClient> and removing the last 100 clients.

Here is the test code. We let the DHT connect for 10 seconds, then kill the last 100 nodes, and see how things evolve in the remaining 900 nodes for some time.

async fn remove_1k() -> TestResult<()> {
    let n = 1000;
    let k = 900;
    let secrets = create_secrets(seed, n);
    let ids = create_node_ids(&secrets);
    // all nodes have all the strategies enabled
    let config = Config::full();
    let (nodes, clients) = create_nodes_and_clients(&ids, next_n(20), config).await;
    for _i in 0..10 {
        tokio::time::sleep(Duration::from_secs(1)).await;
        // write bitmap
    }
    for i in k..n {
        clients.lock().unwrap().remove(&ids[i]);
    }
    for _i in 0..40 {
        tokio::time::sleep(Duration::from_secs(1)).await;
        // write bitmap
    }
    // write animated gif
    Ok(())
}

And here is the resulting gif:

You can clearly see all nodes quickly forgetting about the dead nodes (last 100 pixels in each row). So removal of dead nodes works in principle. You could of course accelerate this by explicitly pinging all routing table entries in regular intervals, but that would be costly, and only gradually forgetting about dead nodes might even have some advantages - there is a grace period where nodes could come back.

What's next?

So now we got a DHT impl and have some reasonable condidence that it works in principle. But all tests use memory connections, which is of course not what is going to be used in production.

The next step is to write tests using actual iroh connections. We will have to deal with real world issues like talking to many nodes without having too many connections open at the same time. And we will move closer to a DHT implementation that can be useful in the messy real world.